Le forze elastiche

Sono dette forze elastiche quelle che si oppongono alla deformazione di un corpo. Tutti i corpi soggetti all'azione di una forza subiscono una deformazione, che dipende, oltre che dall'intensità della forza applicata, anche dalla natura del corpo stesso. In generale, le deformazioni possono essere di due tipi: elastiche, che scompaiono quando la forza non è più applicata, e anelastiche, che permangono anche successivamente all'applicazione della forza.

Dal punto di vista dei corpi, è possibile introdurre una distinzione tra corpi rigidi, plastici ed elastici, sulla base del comportamento del corpo durante e dopo l'applicazione della forza, cioè su quanto esso si sia prima deformato e abbia poi ripreso o meno il suo aspetto iniziale. I corpi rigidi mantengono inalterata la propria forma anche a seguito dell'applicazione di una forza; i corpi plastici, deformati dall'azione di una forza, non riprendono il loro aspetto primitivo; i corpi elastici vengono deformati ma riprendono il loro aspetto primitivo quando viene meno l'azione della forza. Queste proprietà vengono giustificate dal fatto che, a livello microscopico, i corpi solidi sono formati da un insieme di particelle con disposizione spaziale ben definita, all'interno del reticolo cristallino. Quando un corpo si deforma, la disposizione iniziale delle particelle si altera; la sua elasticità è quindi una misura della tendenza del suo reticolo a ricreare la configurazione iniziale. Quando però l'intensità della forza applicata è troppo elevata, tutti i corpi si possono deformare permanentemente e, al limite, rompersi; la deformazione massima a cui un corpo può essere sottoposto senza che esso modifichi permanentemente il proprio aspetto viene detta limite di elasticità.

La legge di Hooke

La formulazione della legge sulle forze elastiche si deve al fisico inglese R. Hooke (1635-1703), il quale stabilì che la forza elastica è direttamente proporzionale all'intensità della deformazione (sempre per valori inferiori al limite di elasticità) ed è sempre opposta a quella che provoca la deformazione stessa. Nel caso di una molla, per esempio, la sua deformazione, cioè il suo allungamento, è maggiore quanto più grande è la forza con cui essa viene tirata. Secondo la legge di Hooke, il modulo della forza elastica è dato dall'espressione:

dove k è una costante positiva, detta costante elastica, caratteristica del materiale considerato, e x il vettore spostamento, che nel caso della molla è pari al suo allungamento. Il segno meno indica che la forza ha verso opposto allo spostamento, opponendosi alle deformazioni con un'intensità a loro direttamente proporzionale, tendente a riportare la molla alla lunghezza iniziale.

Forze elastiche e moto armonico

Il moto armonico può essere cinematicamente rappresentato proiettando istante per istante, sul diametro della circonferenza-traiettoria, un punto P che si muove di moto circolare uniforme. È possibile dimostrare che questo movimento coincide con quello di una molla ideale che, compressa o allungata, tende a tornare alla propria posizione di equilibrio: in altre parole, il movimento dell'immagine del punto P sulla circonferenza è riconducibile all'applicazione di una forza elastica.

L'immagine Q, ottenuta proiettando sul diametro della circonferenza-traiettoria un punto P che si muove di moto circolare uniforme, ha la caratteristica di accelerare avvicinandosi al centro della circonferenza e di rallentare allontanandosene; nelle estremità del diametro, in particolare, si arresta, per poi riprendere con accelerazione di verso opposto. Quando il punto P si muove sulla circonferenza con accelerazione centripeta ap, la sua proiezione Q si muove sul diametro con un'accelerazione aQ, che si ottiene proiettando aP sul diametro. Quando P si muove sulla circonferenza, Q ne segue il comportamento, con un'accelerazione che in ogni istante ha verso opposto a quello dell'accelerazione di P. Esprimendo l'accelerazione centripeta di P in termini di velocità angolare (v=R) si ottiene:

e l'accelerazione della proiezione di P sul diametro è data da:

Questa espressione definisce l'accelerazione di Q come proporzionale rispetto al suo spostamento x dal centro O della circonferenza, ovvero rispetto al centro dell'oscillazione.

Dalla legge fondamentale della dinamica, la forza responsabile dell'oscillazione risulta data da:

che, sostituendo m² con la costante k, rappresenta l'espressione della forza elastica:

Quindi si può dire che un corpo sottoposto a una forza elastica (per esempio, una molla) si muove di moto armonico, con velocità angolare e periodo T rispettivamente uguali a:

Il pendolo

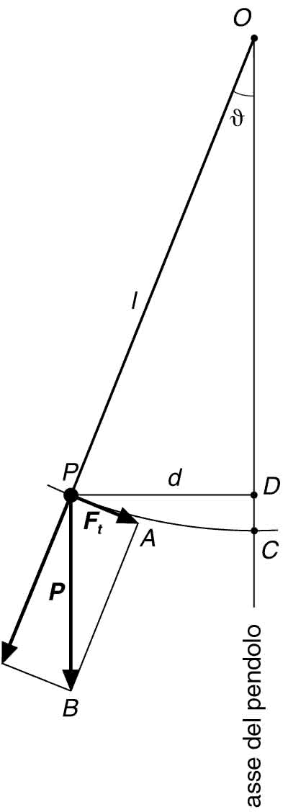
Il più importante esempio di moto armonico è fornito dal cosiddetto pendolo semplice: un corpo P di massa m, appeso a un filo di lunghezza l, fissato a un punto O e lasciato libero di oscillare (v. fig. 5.3). La massa m, spostata di poco dalla sua posizione di equilibrio, tende a oscillare sotto l'azione di una forza elastica, seguendo la legge del moto armonico. Riferendoci alla figura 5.3, la massa m è soggetta alla propria forza peso P, ma di questa solo la componente Ft (perpendicolare al filo e tangente alla traiettoria) è responsabile delle oscillazioni del pendolo, poiché l'azione della componente parallela al filo è annullata dalla corrispondente reazione del filo. Se l'angolo di oscillazione è piccolo, il settore circolare OPC si potrà approssimare al triangolo OPD e scrivere, per la similitudine tra i due triangoli rettangoli PBA e OPD, la proporzione:

Ponendo:

e aggiungendo il segno negativo, a indicare che l'azione di F è in contrasto con lo spostamento, si ritrova la definizione di forza elastica:

dove, sempre per la piccola ampiezza dell'angolo di oscillazione, il segmento d si può approssimare all'ascissa della massa. A questo punto, usando la relazione tra il periodo T del moto armonico e la costante elastica k si ottiene:

Nell'ipotesi delle "piccole oscillazioni", quindi, il periodo non dipende dalla massa del pendolo, ma solo dalla lunghezza del filo e dal valore della locale accelerazione di gravità. Questa legge fu scoperta da Galileo e rappresenta la legge dell'isocronismo del pendolo, che in sostanza afferma che tutte le oscillazioni di un pendolo semplice hanno sempre la stessa durata. Risolvendo rispetto all'accelerazione di gravità si ottiene:

relazione che permette di determinare il valore di g a partire dalle oscillazioni note di un pendolo semplice, fatte salve le correzioni imposte dalla presenza degli attriti.